Tessellation Project
1. What is the idea/theme behind your tessellation?
My theme is a cabin in the woods because I messed around until some ideas came and I realized that
I didn’t have to do anything to complex. I have no relation to the cabin but it just came into my mind
and I went with it.
2. What polygon(s) did you start with and how did you alter it?
I wanted to make my polygon more straight instead of curvy. There are more pointy edges and sharp
angles than I’d like. But I also didn’t want to make it to complex to the point on confusion.
3. In your opinion, are tessellations math or art? Justify your answer.
Tessellations have always been argued it but in my opinion it is both. They have the symmetry and
perfectness of math, but at the same time it has the shapes and illusion of art. People have their
argument that it was created by a mathematician but other argue that anyone could make art. To me
it doesn’t matter which one because they can be both it just matter the perspective you look at it with.
My theme is a cabin in the woods because I messed around until some ideas came and I realized that
I didn’t have to do anything to complex. I have no relation to the cabin but it just came into my mind
and I went with it.
2. What polygon(s) did you start with and how did you alter it?
I wanted to make my polygon more straight instead of curvy. There are more pointy edges and sharp
angles than I’d like. But I also didn’t want to make it to complex to the point on confusion.
3. In your opinion, are tessellations math or art? Justify your answer.
Tessellations have always been argued it but in my opinion it is both. They have the symmetry and
perfectness of math, but at the same time it has the shapes and illusion of art. People have their
argument that it was created by a mathematician but other argue that anyone could make art. To me
it doesn’t matter which one because they can be both it just matter the perspective you look at it with.
Burning Tent Lab
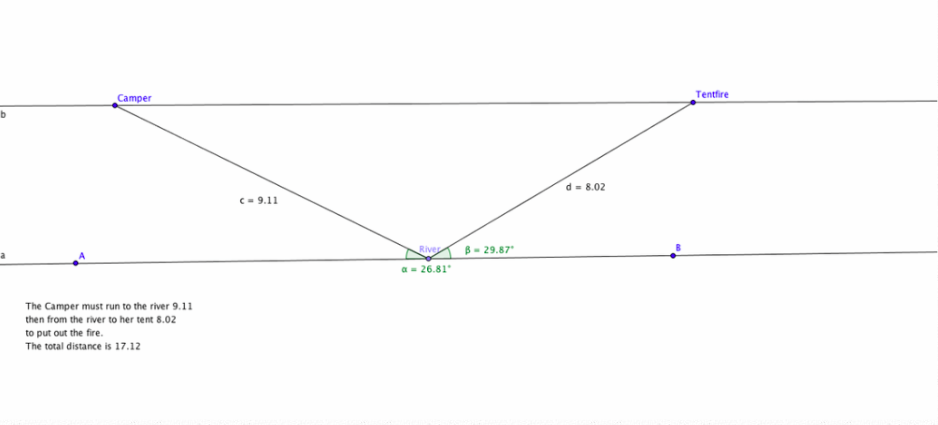
Question 1: Once you have a minimal path, what appears to be true about the incoming angle and the outgoing angle?
Answer: The shortest path is when the outgoing and incoming angles are the same.
Question 2: Why is the path from points Camper to TentFire' the shortest path? Briefly explain. (Think about the shortest distance between two points.)
The shortest path will always be a straight line from the origin to the image.
Question 3: Where should the point River be located in relation to segment Camper to TentFire' and line AB so that the sum of the distances is minimized?
Answer: It should be as close to in the middle as possible.
Answer: The shortest path is when the outgoing and incoming angles are the same.
Question 2: Why is the path from points Camper to TentFire' the shortest path? Briefly explain. (Think about the shortest distance between two points.)
The shortest path will always be a straight line from the origin to the image.
Question 3: Where should the point River be located in relation to segment Camper to TentFire' and line AB so that the sum of the distances is minimized?
Answer: It should be as close to in the middle as possible.
Snail Trail Lab
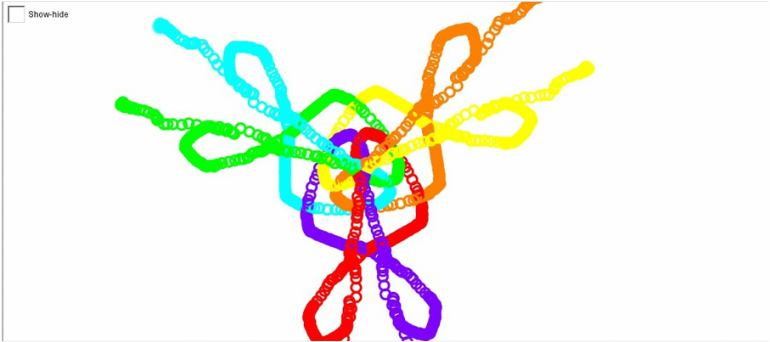
When clicking on the "snails" and dragging them and each one mimics the others.
This creates symmetry in the picture. The colors of each "snail" make it is easy to
tell the were six separate dots, and to show that each one copies the corresponding
dot. If the color was to be removed, there would still be symmetry, but it would change
from rotational to reflection symmetry.
This creates symmetry in the picture. The colors of each "snail" make it is easy to
tell the were six separate dots, and to show that each one copies the corresponding
dot. If the color was to be removed, there would still be symmetry, but it would change
from rotational to reflection symmetry.
POW 2
POW 3

POW Reflection
POWs have helped me mathematically grow by really drilling the information into my head.
We did a total of seven POWs and each was harder and more rigorous than the last. Some
POWs were easier than other and others were harder but I learned from each one and
looked at mathematical situation different because of it.
We did a total of seven POWs and each was harder and more rigorous than the last. Some
POWs were easier than other and others were harder but I learned from each one and
looked at mathematical situation different because of it.
Unit 4 - Desmos Drawing and Function Families
Link to Project: https://www.desmos.com/calculator/0cvnjojguv
Reflection
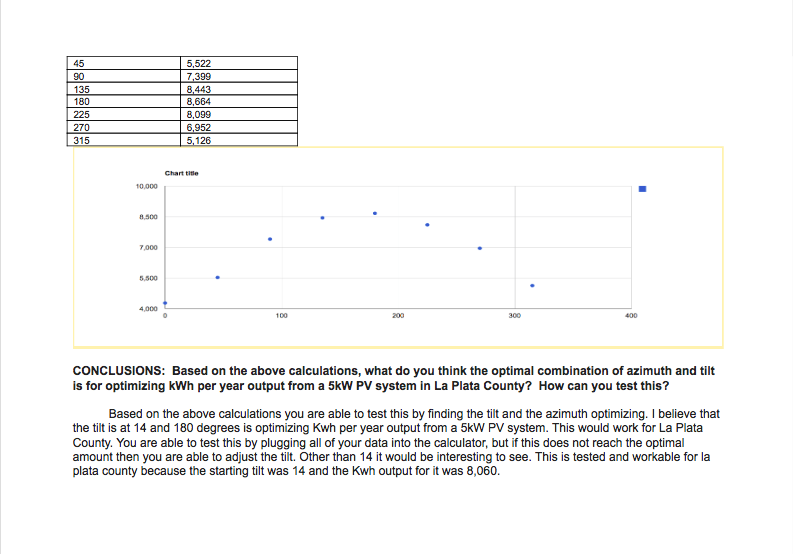
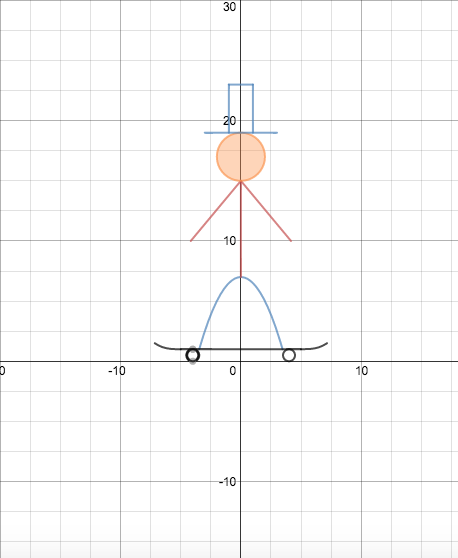
My main problem was trying to figure out how to incorporate a quadratic function into my drawing. I planed to do a skateboarder but I didn’t sketch it out before I just went along and revised throughout the process. I experimented with different sizes of shapes to find the most symmetrical for a stick body. I did ask a few people what I could do to add to it and I got the suggestion to add the top hat.
Desmos helped my understanding slightly but I will never completely memorize all the functions. I did get quadratic functions a lot more even though I just had two. I did spend more time on them than any other function though. I learn quadratic functions can be manipulated to any type of curve or line depending on the change of numbers within the function.
Desmos helped my understanding slightly but I will never completely memorize all the functions. I did get quadratic functions a lot more even though I just had two. I did spend more time on them than any other function though. I learn quadratic functions can be manipulated to any type of curve or line depending on the change of numbers within the function.
Shadows, Similarity and Right Triangle Trigonometry
Q1: What has been the work you are most proud of in this unit?
I am most proud of the Slices of Pie POW. We had to find the most amount of slices with a certain number of cuts. I worked hard on it although I only got a 19/25 because I got the wrong answer on it.
Q2: What skills are you developing in geometry/math? Skills can be applied across mathematics – think graphing, creating tables, creating diagrams or mathematical models, approaching problems in different ways (by testing cases, by testing extreme examples, by setting up a table initiating/approaching hard problems, e), or learning how to use your graphing calculator to fit equations to data.
I gained the skills of peer collaboration. It not exactly a mathematical skill but it will be very useful in any class. I will continue to refine this skill throughout my High School years. Using POWs and other group problem was the highlight of this class because of the new perspective others bring to the table.
Q3: Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world (i.e. scaled replicas of sculptures, scaled models for architecture, trigonometry in construction or blood splatter analysis, etc).
Trigonometry is the use of COS, SIN, or TAN to solve a certain side of a triangle. Depending of witch side you'd use a different formula. This can be used in construction, engineering, math-related jobs, and designing anything.
I am most proud of the Slices of Pie POW. We had to find the most amount of slices with a certain number of cuts. I worked hard on it although I only got a 19/25 because I got the wrong answer on it.
Q2: What skills are you developing in geometry/math? Skills can be applied across mathematics – think graphing, creating tables, creating diagrams or mathematical models, approaching problems in different ways (by testing cases, by testing extreme examples, by setting up a table initiating/approaching hard problems, e), or learning how to use your graphing calculator to fit equations to data.
I gained the skills of peer collaboration. It not exactly a mathematical skill but it will be very useful in any class. I will continue to refine this skill throughout my High School years. Using POWs and other group problem was the highlight of this class because of the new perspective others bring to the table.
Q3: Choose one topic: similarity (ratios) or trigonometry. Explain what it is. Provide an example of how it is used in mathematics to solve problems. State an application of the topic in the adult world (i.e. scaled replicas of sculptures, scaled models for architecture, trigonometry in construction or blood splatter analysis, etc).
Trigonometry is the use of COS, SIN, or TAN to solve a certain side of a triangle. Depending of witch side you'd use a different formula. This can be used in construction, engineering, math-related jobs, and designing anything.
Unit 3 Reflection: Area, Volume, Measurement
Q1: What content/skills have been most interesting to you?
Visualizing 3-d shapes was the hardest for me so it was challenging for me to get it down. Even though we didn't go over it very much I still tried to get it down based on the fact it is one of the most useful thing to be able to look at something 2-d then shape it into something 3-d. By the end of the unit I got to fully understood them and was ready to move onto the next subject.
Q2: How have you grown mathematically?
I have grown mathematical because I have learned how equation corollate to graphs. We learn the different equations for different types of lines like quadratic, linear, and cubic function. The desmos project helped me the most with this and doing it over and over really made me get it down.
Visualizing 3-d shapes was the hardest for me so it was challenging for me to get it down. Even though we didn't go over it very much I still tried to get it down based on the fact it is one of the most useful thing to be able to look at something 2-d then shape it into something 3-d. By the end of the unit I got to fully understood them and was ready to move onto the next subject.
Q2: How have you grown mathematically?
I have grown mathematical because I have learned how equation corollate to graphs. We learn the different equations for different types of lines like quadratic, linear, and cubic function. The desmos project helped me the most with this and doing it over and over really made me get it down.